3d Geometrical Transformation Matrix If Know Two Vectors

By pre multiplying both sides of these equations by the inverse of q q 1.
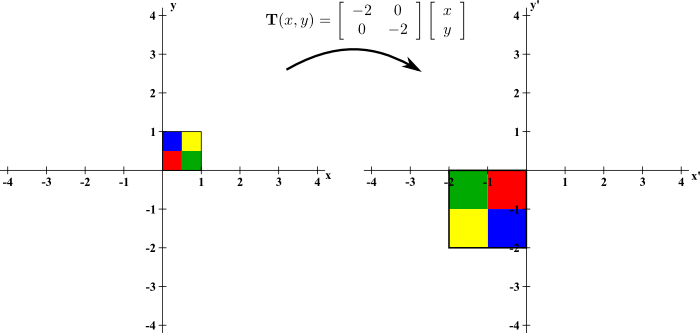
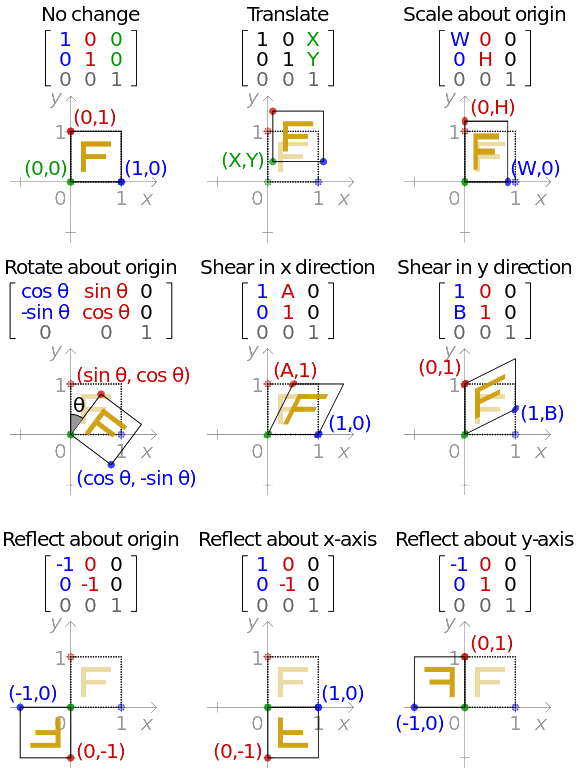
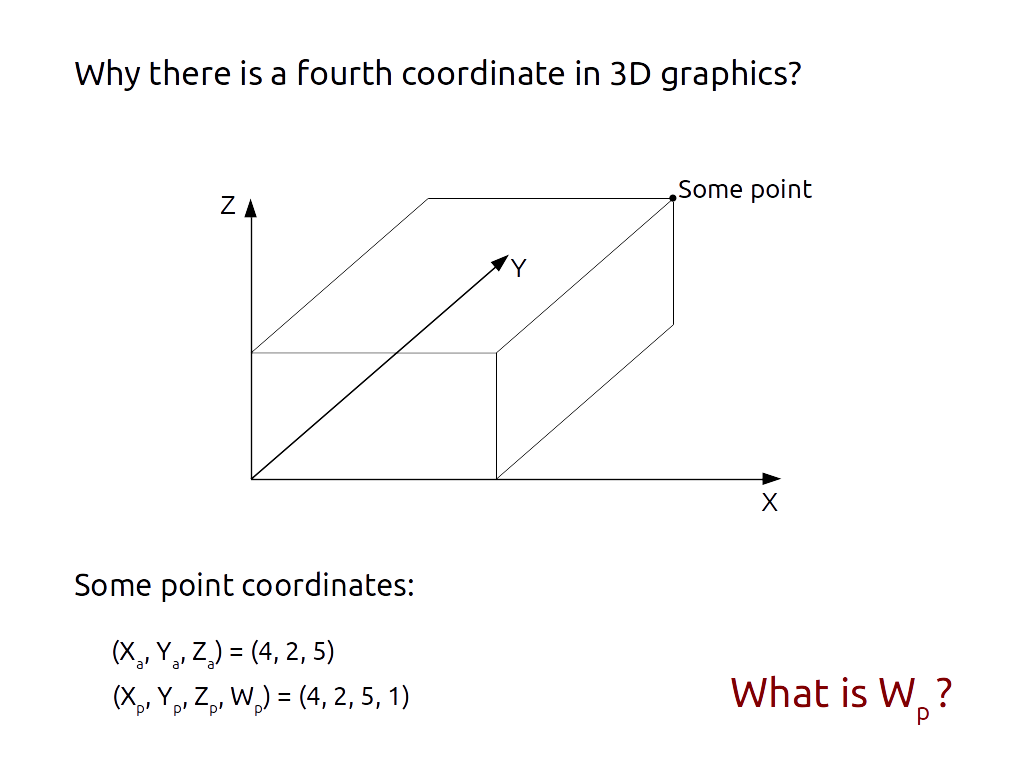
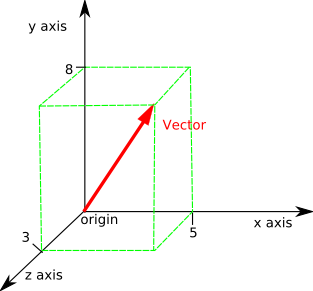
3d geometrical transformation matrix if know two vectors. Rotation is a complicated scenario for 3d transforms. T x t y t z are translation vectors in x y and z directions respectively. W au bv where a and b are arbitrary scalars. In the graph above x 1 0 y 1 0 and x 2 2 y 2 5.
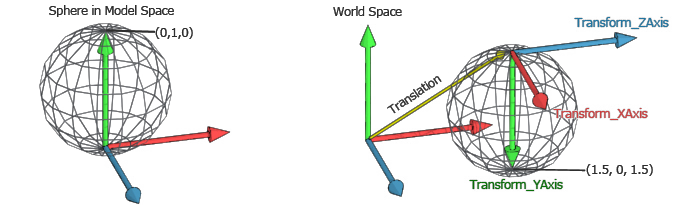
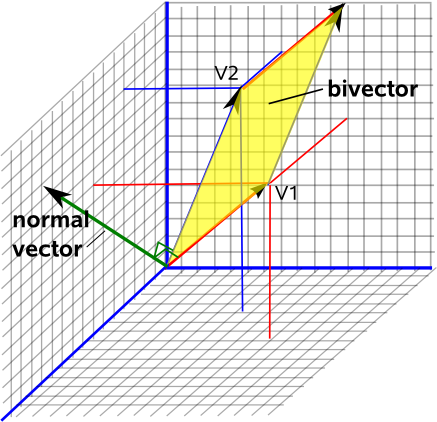
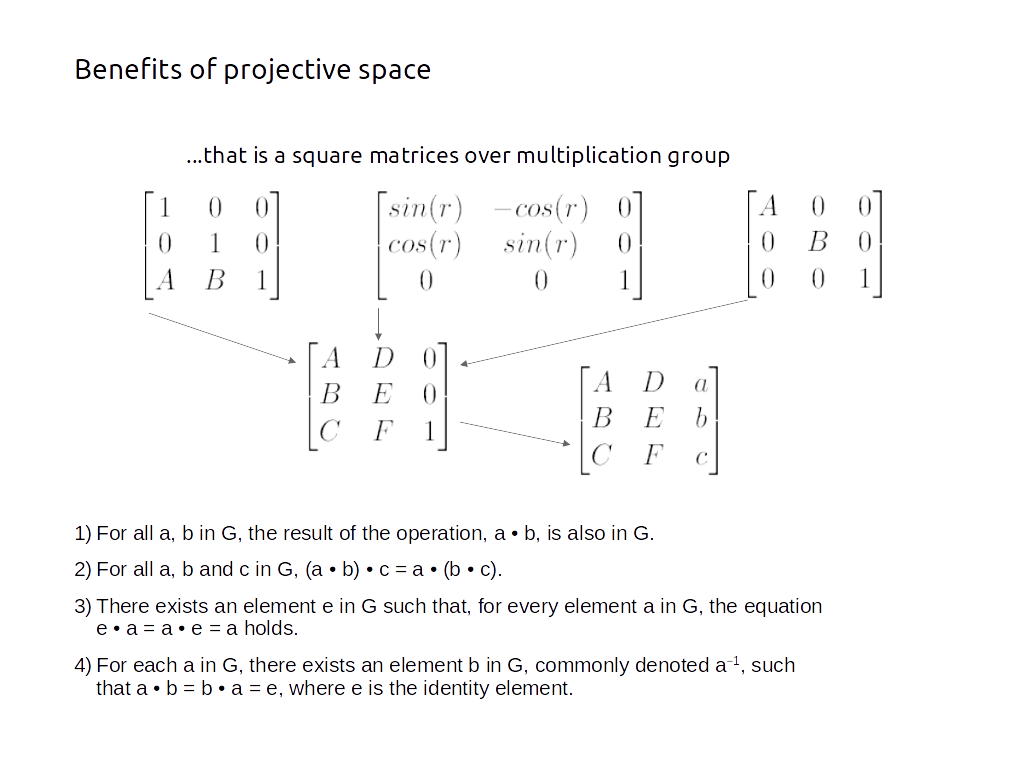
For example if you have two vectors u and v then a third vector w can be constructed via a linear combination of u and v. Geometry of the 2d coordinate transformation. 2 2 matrix is called the or rotationtransformation matrix q. If an object has five corners then the translation will be accomplished by translating all five points to new locations.
In matrix form these transformation equations can be written as. 11 22 cos sin sin cos u u u u θθ θθ 1 5 3 figure 1 5 3. I know this is a mouthful but what it really just means scaling terms adding them together. Again we must translate an object so that its center lies on the origin before scaling it.
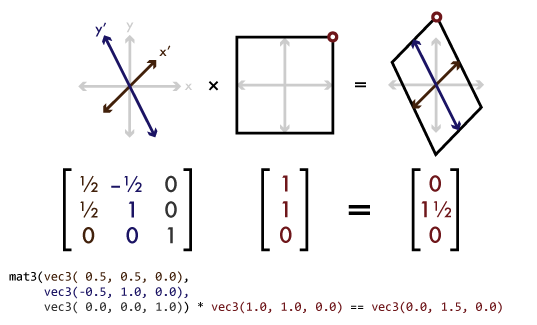
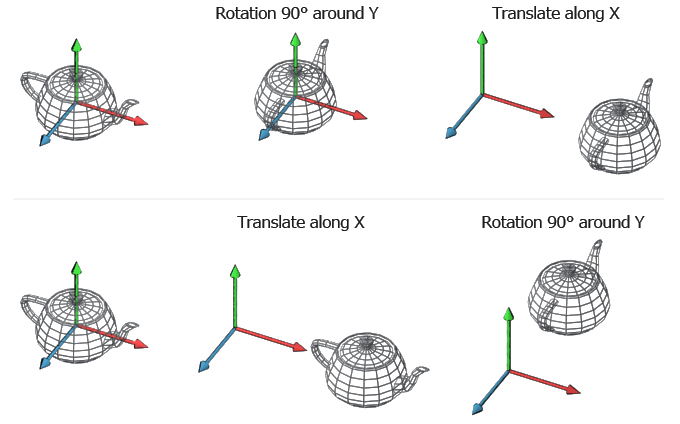
X 1 x t x y 1 y t y z 1 z t z. In linear algebra linear transformations can be represented by matrices if is a linear transformation mapping to and is a column vector with entries then for some matrix called the transformation matrix of note that has rows and columns whereas the transformation is from to there are alternative expressions of transformation matrices involving row vectors that are. Lecture l3 vectors matrices and coordinate transformations by using vectors and defining appropriate operations between them physical laws can often be written in a simple form. Matrix multiplication is not in general commutative.
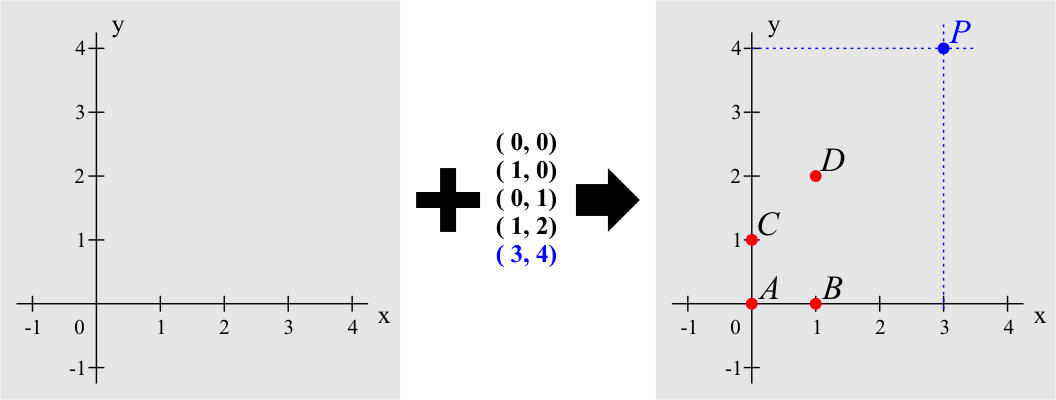
Since we will making extensive use of vectors in dynamics we will summarize some of their important properties. The component form of a vector is the ordered pair that describes the changes in the x and y values.