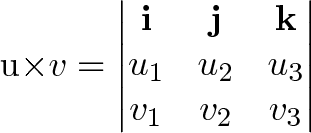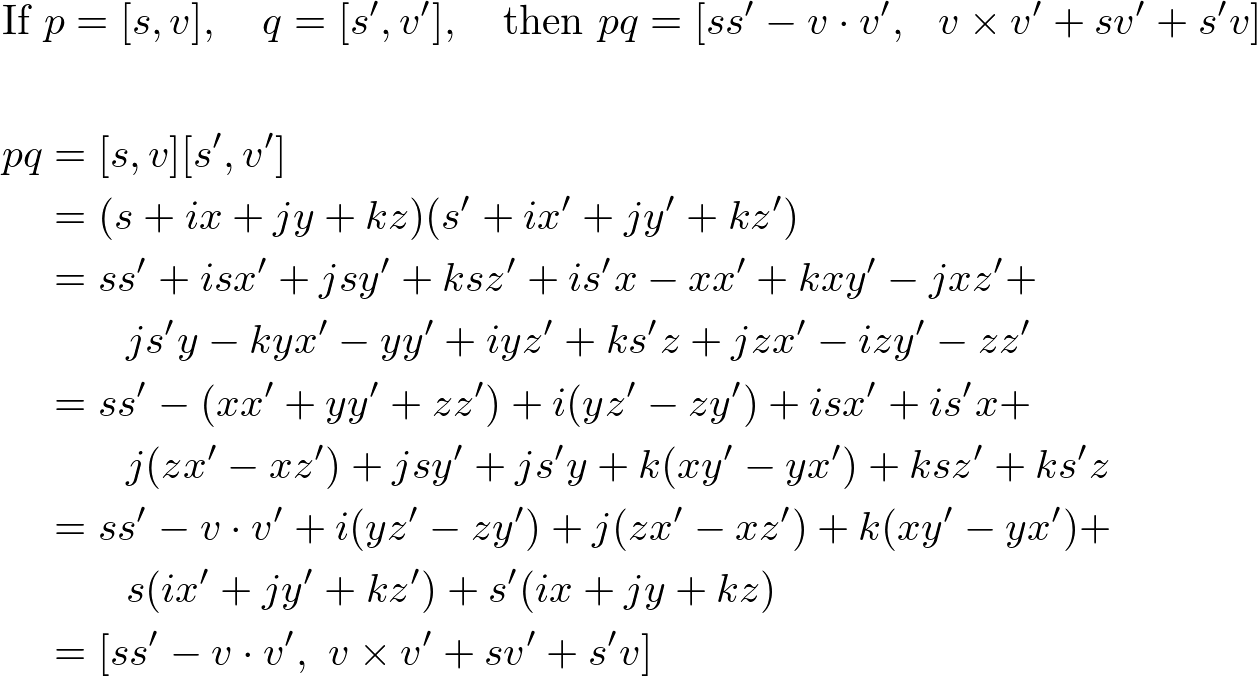Multiplying 3d Vectors

For example finding the distance of a point from a plane or from a line or the shortest distance between two lines in space or the equation of a plane defined by three points.
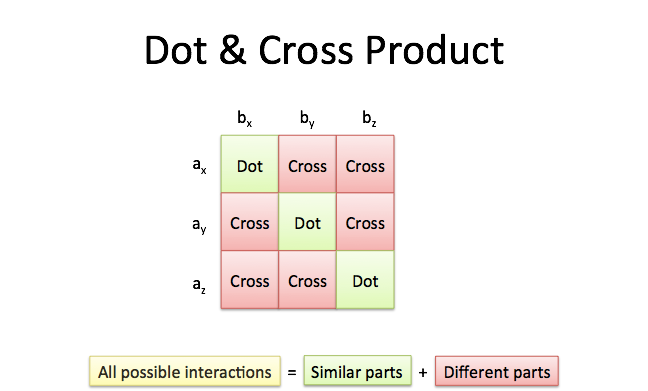
Multiplying 3d vectors. We can draw the vector op as follows. We saw earlier how to represent 2 dimensional vectors on the x y plane. First of all what s a plane. Use value and value spectral to get the dot product.
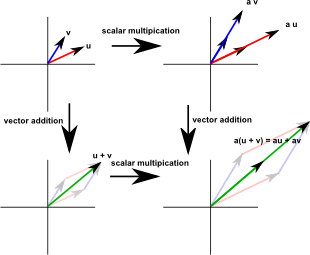
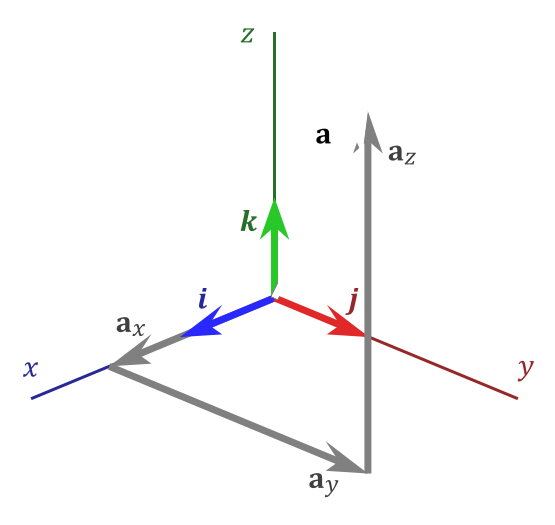
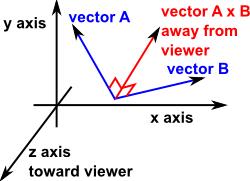
Use two normalize 3d vector nodes to get the absolute values lengths from the vectors and multiply them with another value. Now we extend the idea to represent 3 dimensional vectors using the x y z axes. And to divide the vector with we can simply multiply the vector with. The magnitude of the vector formed by multiplying and is the magnitude of multiplied by and the direction of the vector is same as vector if is positive and exactly oppsite of is negative.
The vector op has initial point at the origin o 0 0 0 and terminal point at p 2 3 5. If we multiply a vector by a scalar then the result is a new vector. Since it is just as easy to work with vectors in 3 dimensions as in 2 dimensions you will find that most 3d geometry is done using vectors and the dot product turns up in just about every problem you can think of. The term arccos a in expr value node gives phi in radian from 0 to pi.
See the 3 dimensional co ordinate system for background on this.